Modern Methods of Integral Calculation

A research team from the Netrix S.A. Research and Development Center and the WSEI Academy in Lublin, consisting of Dr. hab. Eng. Tomasz Rymarczyk and Prof. Eng. Jan Sikora, presented a groundbreaking approach to the numerical integration of functions with logarithmic singularities in the context of the Boundary Element Method (BEM). In the published paper “Some More on Logarithmic Singularity Integration in Boundary Element Method,” the authors introduce innovative computational techniques that significantly enhance the precision and efficiency of engineering simulations, particularly in acoustic applications.

The primary aim of the research was to analyze the effectiveness of two approaches to handling singularities in boundary integrals. The first method, the singularity-ignoring technique, involves the standard use of an increased number of Gauss integration points. Although simple to implement, this technique is associated with high computational costs, especially for meshes containing higher-order elements. An alternative is the singularity subtraction technique, which allows for the precise separation of the singular component from the regular part. This solution enables much greater computational accuracy while simultaneously reducing the number of numerical operations, making it particularly attractive for the analysis of complex boundary problems.

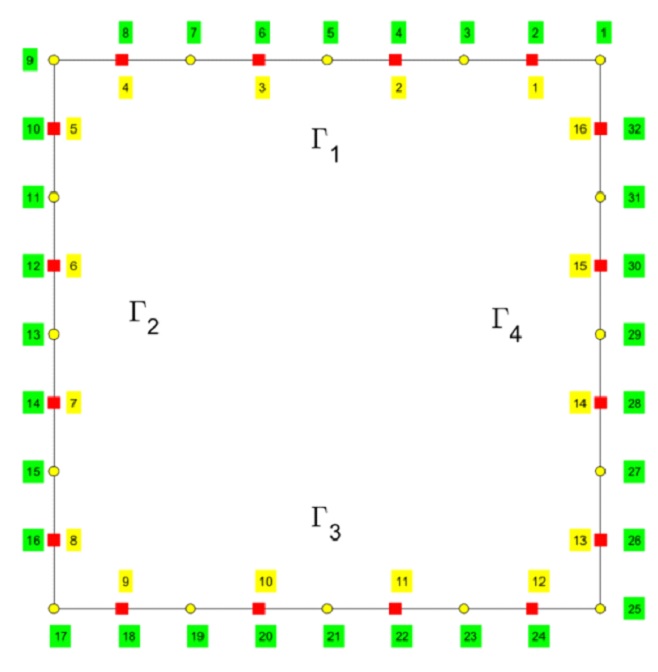
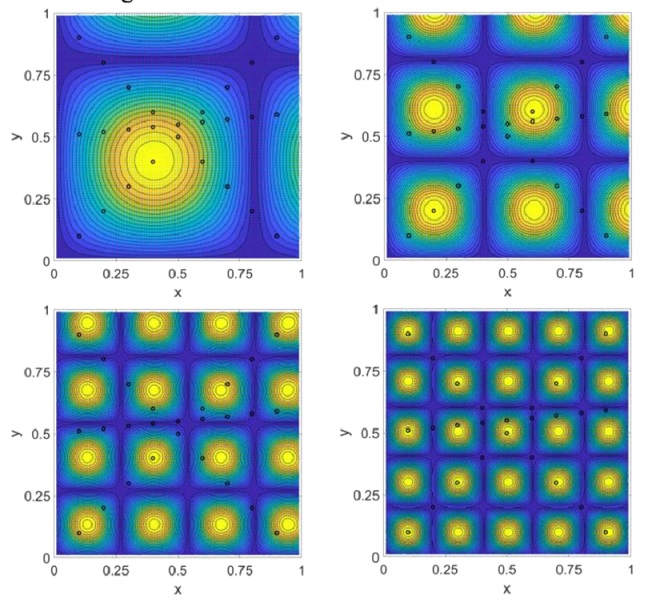
*Example of discretization of a homogeneous domain using second-order boundary elements with node and element numbering.*

*Area of interest and distribution of equipotential lines for different excitation frequencies.*

W pracy omówiono również wpływ różnych parametrów fizycznych i geometrycznych na skuteczność całkowania. Dotyczy to m.in. częstotliwości fali akustycznej oraz obecności ostrych krawędzi w analizowanym obszarze. W kontekście zagadnień akustycznych opisywanych równaniem Helmholtza, zastosowanie metody odejmowania osobliwości umożliwiło uzyskanie średniego błędu względnego (MRE) na poziomie 1–5%, nawet przy wysokich częstotliwościach. Dodatkowo, badania objęły zarówno problemy Dirichleta, jak i szeroki zakres zagadnień z zakresu propagacji fal.

These results have direct implications for engineering practice. The Boundary Element Method (BEM) is applied in many fields: from the design of acoustic systems, through electromagnetic field analysis, to the modeling of thermal and mechanical phenomena. The developed computational techniques not only increase the precision of simulations but also accelerate the design process, enabling faster and more reliable testing of different configurations.

A particularly interesting aspect is the ability to analytically calculate the singular component in the case of Laplace’s equations, which significantly speeds up integration procedures. Such solutions contribute to the further development of numerical tools, improving their quality and usefulness in modern engineering.

The full version of the article is available at:
link to publication